圖執行模式下的 TensorFlow 2¶
儘管 TensorFlow 2 建議以即時執行模式(Eager Execution)作為主要執行模式,然而,圖執行模式(Graph Execution)作為 TensorFlow 2 之前的主要執行模式,依舊對於我們理解 TensorFlow 具有重要意義。尤其是當我們需要使用 tf.function 時,對圖執行模式的理解更是不可或缺。
圖執行模式在 TensorFlow 1.X 和 2.X 版本中的 API 不同:
在 TensorFlow 1.X 中,圖執行模式主要通過「直接建構計算圖 +
tf.Session」 進行操作;在 TensorFlow 2 中,圖執行模式主要通過
tf.function進行操作。
在本章,我們將在 tf.function:圖執行模式 一節的基礎上,進一步對圖執行模式的這兩種 API 進行對比說明,以幫助已熟悉 TensorFlow 1.X 的用戶過渡到 TensorFlow 2。
提示
TensorFlow 2 依然支持 TensorFlow 1.X 的 API。為了在 TensorFlow 2 中使用 TensorFlow 1.X 的 API ,我們可以使用 import tensorflow.compat.v1 as tf 導入 TensorFlow,並通過 tf.disable_eager_execution() 禁用默認的即時執行模式。
TensorFlow 1+1¶
TensorFlow 的圖執行模式是一個符號式的(基於計算圖的)計算框架。簡而言之,如果你需要進行一系列計算,則需要依次進行如下兩步:
建立一個「計算圖」,這個圖描述了如何將輸入資料通過一系列計算而得到輸出;
建立一個會話,並在會話中與計算圖進行交互,即向計算圖傳入計算所需的資料,並從計算圖中獲取結果。
使用計算圖進行基本運算¶
這裡以計算 1+1 作為 Hello World 的示例。以下程式碼通過 TensorFlow 1.X 的圖執行模式 API 計算 1+1:
import tensorflow.compat.v1 as tf
tf.disable_eager_execution()
# 以下三行定義了一個簡單的“計算圖”
a = tf.constant(1) # 定義一個常數變數(Tensor)
b = tf.constant(1)
c = a + b # 等同於 c = tf.add(a, b),c是變數a和變數b通過 tf.add 這一操作(Operation)所形成的新變數
# 到此為止,計算圖定義完畢,然而程式還沒有進行任何實質計算。
# 如果此時直接輸出變數 c 的值,是無法獲得 c = 2 的結果的
sess = tf.Session() # 實例化一個會話(Session)
c_ = sess.run(c) # 通過會話的 run() 方法對計算圖里的節點(變數)進行實際的計算
print(c_)
輸出:
2
而在 TensorFlow 2 中,我們將計算圖的建立步驟封裝在一個函數中,並使用 @tf.function 修飾符對函數進行修飾。當需要運行此計算圖時,只需呼叫修飾後的函數即可。由此,我們可以將以上程式碼改寫如下:
import tensorflow as tf
# 以下被 @tf.function 修飾的函數定義了一個計算圖
@tf.function
def graph():
a = tf.constant(1)
b = tf.constant(1)
c = a + b
return c
# 到此為止,計算圖定義完畢。由於 graph() 是一個函數,在其被呼叫之前,程式是不會進行任何實質計算的。
# 只有呼叫函數,才能通過函數取得回傳值,取得 c = 2 的結果
c_ = graph()
print(c_.numpy())
小結
在 TensorFlow 1.X 的 API 中,我們直接在主程序中建立計算圖。而在 TensorFlow 2 中,計算圖的建立需要被封裝在一個被
@tf.function修飾的函數中;在 TensorFlow 1.X 的 API 中,我們通過實例化一個
tf.Session,並使用其run方法執行計算圖的實際運算。而在 TensorFlow 2 中,我們通過直接呼叫被@tf.function修飾的函數來執行實際運算。
計算圖中的占位符與資料輸入¶
上面這個程序只能計算1+1,以下程式碼通過 TensorFlow 1.X 的圖執行模式 API 中的 tf.placeholder() (占位符張量)和 sess.run() 的 feed_dict 參數,展示了如何使用TensorFlow計算任意兩個數的和:
import tensorflow.compat.v1 as tf
tf.disable_eager_execution()
a = tf.placeholder(dtype=tf.int32) # 定義一個字符串Tensor
b = tf.placeholder(dtype=tf.int32)
c = a + b
a_ = int(input("a = ")) # 從使用者讀入一個整數並放入變數a_
b_ = int(input("b = "))
sess = tf.Session()
c_ = sess.run(c, feed_dict={a: a_, b: b_}) # feed_dict參數傳入為了計算c所需要的變數的值
print("a + b = %d" % c_)
運行程序:
>>> a = 2
>>> b = 3
a + b = 5
而在 TensorFlow 2 中,我們可以通過為函數指定參數來實現與占位符張量相同的功能。為了在計算圖運行時送入占位符資料,只需在呼叫被修飾後的函數時,將資料作為參數傳入即可。由此,我們可以將以上程式碼改寫如下:
import tensorflow as tf
@tf.function
def graph(a, b):
c = a + b
return c
a_ = int(input("a = "))
b_ = int(input("b = "))
c_ = graph(a_, b_)
print("a + b = %d" % c_)
小結
在 TensorFlow 1.X 的 API 中,我們使用 tf.placeholder() 在計算圖中宣告占位符張量,並通過 sess.run() 的 feed_dict 參數向計算圖中的占位符傳入實際資料。而在 TensorFlow 2 中,我們使用 tf.function 的函數參數作為占位符張量,通過向被 @tf.function 修飾的函數傳遞參數,來為計算圖中的占位符張量提供實際資料。
計算圖中的變數¶
變數的宣告¶
變數 (Variable)是一種特殊類型的張量,在 TensorFlow 1.X 的圖執行模式 API 中使用 tf.get_variable() 建立。與程式語言中的變數很相似。使用變數前需要先初始化,變數內存儲的值可以在計算圖的計算過程中被修改。以下示例程式碼展示了如何建立一個變數,將其值初始化為0,並逐次累加1。
import tensorflow.compat.v1 as tf
tf.disable_eager_execution()
a = tf.get_variable(name='a', shape=[])
initializer = tf.assign(a, 0.0) # tf.assign(x, y)返回一個“將變數y的值指定給變數x”的操作
plus_one_op = tf.assign(a, a + 1.0)
sess = tf.Session()
sess.run(initializer)
for i in range(5):
sess.run(plus_one_op) # 對變數a執行此一操作
print(sess.run(a)) # 輸出此時變數a在當前會話的計算圖的值
輸出:
1.0
2.0
3.0
4.0
5.0
提示
為了初始化變數,也可以在宣告變數時指定初始化器(initializer),並通過 tf.global_variables_initializer() 一次性初始化所有變數,在實際工程中更常用:
import tensorflow.compat.v1 as tf
tf.disable_eager_execution()
a = tf.get_variable(name='a', shape=[],
initializer=tf.zeros_initializer) # 指定初始化器為全0初始化
plus_one_op = tf.assign(a, a + 1.0)
sess = tf.Session()
sess.run(tf.global_variables_initializer()) # 初始化所有變數
for i in range(5):
sess.run(plus_one_op)
print(sess.run(a))
在 TensorFlow 2 中,我們通過實例化 tf.Variable 類來宣告變數。由此,我們可以將以上程式碼改寫如下:
import tensorflow as tf
a = tf.Variable(0.0)
@tf.function
def plus_one_op():
a.assign(a + 1.0)
return a
for i in range(5):
plus_one_op()
print(a.numpy())
小結
在 TensorFlow 1.X 的 API 中,我們使用 tf.get_variable() 在計算圖中宣告變數節點。而在 TensorFlow 2 中,我們直接通過 tf.Variable 實例化變數對象,並在計算圖中使用這一變數對象。
變數的作用域與重用¶
在 TensorFlow 1.X 中,我們建立模型時經常需要指定變數的作用域,以及複用變數。此時,TensorFlow 1.X 的圖執行模式 API 為我們提供了 tf.variable_scope() 及 reuse 參數來實現變數作用域和複用變數的功能。以下的例子使用了 TensorFlow 1.X 的圖執行模式 API 建立了一個三層的全連接神經網絡,其中第三層複用了第二層的變數。
import tensorflow.compat.v1 as tf
import numpy as np
tf.disable_eager_execution()
def dense(inputs, num_units):
weight = tf.get_variable(name='weight', shape=[inputs.shape[1], num_units])
bias = tf.get_variable(name='bias', shape=[num_units])
return tf.nn.relu(tf.matmul(inputs, weight) + bias)
def model(inputs):
with tf.variable_scope('dense1'): # 限定變數的作用為 dense1
x = dense(inputs, 10) # 宣告 dense1/weight 和 dense1/bias 兩個變量
with tf.variable_scope('dense2'): # 限定變數的作用為 dense2
x = dense(x, 10) # 宣告 dense2/weight 和 dense2/bias 兩個變數
with tf.variable_scope('dense2', reuse=True): # 第三層重複使用第二層的變數
x = dense(x, 10)
return x
inputs = tf.placeholder(shape=[10, 32], dtype=tf.float32)
outputs = model(inputs)
print(tf.global_variables()) # 輸出當前計算圖中的所有變數節點
sess = tf.Session()
sess.run(tf.global_variables_initializer())
outputs_ = sess.run(outputs, feed_dict={inputs: np.random.rand(10, 32)})
print(outputs_)
在上例中,計算圖的所有變數節點為:
[<tf.Variable 'dense1/weight:0' shape=(32, 10) dtype=float32>,
<tf.Variable 'dense1/bias:0' shape=(10,) dtype=float32>,
<tf.Variable 'dense2/weight:0' shape=(10, 10) dtype=float32>,
<tf.Variable 'dense2/bias:0' shape=(10,) dtype=float32>]
可見, tf.variable_scope() 為在其上下文中的,以 tf.get_variable 建立的變數的名稱添加了「前綴」或「作用域」,使得變數在計算圖中的層次結構更為清晰,不同「作用域」下的同名變數各司其職,不會衝突。同時,雖然我們在上例中呼叫了3次 dense 函數,即呼叫了6次 tf.get_variable 函數,但實際建立的變數節點只有4個。這即是 tf.variable_scope() 的 reuse 參數所起到的作用。當 reuse=True 時, tf.get_variable 遇到重名變數時將會自動獲取先前建立的同名變數,而不會新建變數,從而達到了變數重用的目的。
而在 TensorFlow 2 的圖執行模式 API 中,不再鼓勵使用 tf.variable_scope() ,而應當使用 tf.keras.layers.Layer 和 tf.keras.Model 來封裝程式碼和指定作用域,具體可參考 本手冊第三章。上面的例子與下面基於 tf.keras 和 tf.function 的程式碼等價。
import tensorflow as tf
import numpy as np
class Dense(tf.keras.layers.Layer):
def __init__(self, num_units, **kwargs):
super().__init__(**kwargs)
self.num_units = num_units
def build(self, input_shape):
self.weight = self.add_variable(name='weight', shape=[input_shape[-1], self.num_units])
self.bias = self.add_variable(name='bias', shape=[self.num_units])
def call(self, inputs):
y_pred = tf.matmul(inputs, self.weight) + self.bias
return y_pred
class Model(tf.keras.Model):
def __init__(self):
super().__init__()
self.dense1 = Dense(num_units=10, name='dense1')
self.dense2 = Dense(num_units=10, name='dense2')
@tf.function
def call(self, inputs):
x = self.dense1(inputs)
x = self.dense2(inputs)
x = self.dense2(inputs)
return x
model = Model()
print(model(np.random.rand(10, 32)))
我們可以注意到,在 TensorFlow 2 中,變數的作用域以及複用變數的問題自然地淡化了。基於Python類的模型建立方式自然地為變數指定了作用域,而變數的重用也可以通過簡單地多次呼叫同一個層來實現。
為了詳細了解上面的程式碼對變數作用域的處理方式,我們使用 get_concrete_function 導出計算圖,並輸出計算圖中的所有變數節點:
graph = model.call.get_concrete_function(np.random.rand(10, 32))
print(graph.variables)
輸出如下:
(<tf.Variable 'dense1/weight:0' shape=(32, 10) dtype=float32, numpy=...>,
<tf.Variable 'dense1/bias:0' shape=(10,) dtype=float32, numpy=...>,
<tf.Variable 'dense2/weight:0' shape=(32, 10) dtype=float32, numpy=...>,
<tf.Variable 'dense2/bias:0' shape=(10,) dtype=float32, numpy=...)
可見,TensorFlow 2 的圖執行模式在變數的作用域上與 TensorFlow 1.X 實際保持了一致。我們通過 name 參數為每個層指定的名稱將成為層內變數的作用域。
小結
在 TensorFlow 1.X 的 API 中,使用 tf.variable_scope() 及 reuse 參數來實現變數作用域和複用變數的功能。在 TensorFlow 2 中,使用 tf.keras.layers.Layer 和 tf.keras.Model 來封裝程式碼和指定作用域,從而使變數的作用域以及複用變數的問題自然淡化。兩者的實質是一樣的。
自動求導機制與優化器¶
在本節中,我們對 TensorFlow 1.X 和 TensorFlow 2 在圖執行模式下的自動求導機制進行較深入的比較說明。
自動求導機制¶
我們首先回顧 TensorFlow 1.X 中的自動求導機制。在 TensorFlow 1.X 的圖執行模式 API 中,可以使用 tf.gradients(y, x) 計算計算圖中的張量節點 y 相對於變數 x 的導數。以下示例展示了在 TensorFlow 1.X 的圖執行模式 API 中計算 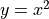 在
在 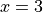 時的導數。
時的導數。
x = tf.get_variable('x', dtype=tf.float32, shape=[], initializer=tf.constant_initializer(3.))
y = tf.square(x) # y = x ^ 2
y_grad = tf.gradients(y, x)
以上程式碼中,計算圖中的節點 y_grad 即為 y 相對於 x 的導數。
而在 TensorFlow 2 的圖執行模式 API 中,我們使用 tf.GradientTape 這一上下文管理器封裝需要求導的計算步驟,並使用其 gradient 方法求導,程式碼示例如下:
x = tf.Variable(3.)
@tf.function
def grad():
with tf.GradientTape() as tape:
y = tf.square(x)
y_grad = tape.gradient(y, x)
return y_grad
小結
在 TensorFlow 1.X 中,我們使用 tf.gradients() 求導。而在 TensorFlow 2 中,我們使用使用 tf.GradientTape 這一上下文管理器封裝需要求導的計算步驟,並使用其 gradient 方法求導。
優化器¶
由於機器學習中的求導往往伴隨著優化,所以 TensorFlow 中更常用的是優化器(Optimizer)。在 TensorFlow 1.X 的圖執行模式 API 中,我們往往使用 tf.train 中的各種優化器,將求導和調整變數值的步驟合二為一。例如,以下程式碼片段在計算圖建構過程中,使用 tf.train.GradientDescentOptimizer 這一梯度下降優化器優化損失函數 loss :
y_pred = model(data_placeholder) # 模型建構
loss = ... # 計算模型的損失函數 loss
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.001)
train_one_step = optimizer.minimize(loss)
# 上面一步也可拆分為
# grad = optimizer.compute_gradients(loss)
# train_one_step = optimizer.apply_gradients(grad)
以上程式碼中, train_one_step 即為一個將求導和變數值更新合二為一的計算圖節點(操作),也就是訓練過程中的「一步」。特別需要注意的是,對於優化器的 minimize 方法而言,只需要指定待優化的損失函數張量節點 loss 即可,求導的變數可以自動從計算圖中獲得(即 tf.trainable_variables )。在計算圖建構完成後,只需啓動對話,使用 sess.run 方法運行 train_one_step 這一計算圖節點,並通過 feed_dict 參數送入訓練資料,即可完成一步訓練。程式碼片段如下:
for data in dataset:
data_dict = ... # 將訓練所需資料放入字典 data 內
sess.run(train_one_step, feed_dict=data_dict)
而在 TensorFlow 2 的 API 中,無論是圖執行模式還是即時執行模式,均先使用 tf.GradientTape 進行求導操作,然後再使用優化器的 apply_gradients 方法應用已求得的導數,進行變數值的更新。也就是說,和 TensorFlow 1.X 中優化器的 compute_gradients + apply_gradients 十分類似。同時,在 TensorFlow 2 中,無論是求導還是使用導數更新變數值,都需要顯式地指定變數。計算圖的建構程式碼結構如下:
optimizer = tf.keras.optimizer.SGD(learning_rate=...)
@tf.function
def train_one_step(data):
with tf.GradientTape() as tape:
y_pred = model(data) # 模型建構
loss = ... # 計算模型的損失函數 loss
grad = tape.gradient(loss, model.variables)
optimizer.apply_gradients(grads_and_vars=zip(grads, model.variables))
在計算圖建構完成後,我們直接呼叫 train_one_step 函數並送入訓練資料即可:
for data in dataset:
train_one_step(data)
小結
在 TensorFlow 1.X 中,我們多使用優化器的 minimize 方法,將求導和變數值更新合二為一。而在 TensorFlow 2 中,我們需要先使用 tf.GradientTape 進行求導操作,然後再使用優化器的 apply_gradients 方法應用已求得的導數,進行變數值的更新。而且在這兩步中,都需要顯式指定待求導和待更新的變數。
自動求導機制的計算圖對比 *¶
在本節,為了幫助讀者更深刻地理解 TensorFlow 的自動求導機制,我們以前節的「計算 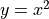 在
在 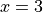 時的導數」為例,展示 TensorFlow 1.X 和 TensorFlow 2 在圖執行模式下,為這一求導過程所建立的計算圖,並進行詳細講解。
時的導數」為例,展示 TensorFlow 1.X 和 TensorFlow 2 在圖執行模式下,為這一求導過程所建立的計算圖,並進行詳細講解。
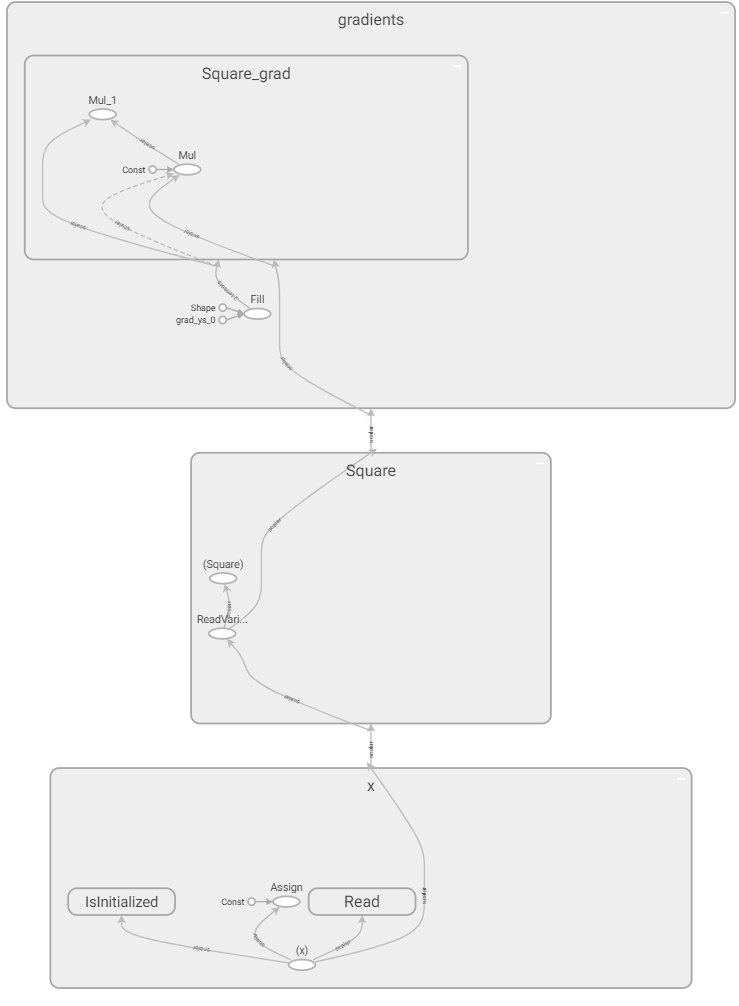
在 TensorFlow 1.X 的圖執行模式 API 中,將生成的計算圖使用 TensorBoard 進行展示:
在計算圖中,灰色的塊為節點的命名空間(Namespace,後文簡稱「塊」),橢圓形代表操作節點(OpNode),圓形代表常量,灰色的箭頭代表資料流。為了弄清計算圖節點 x 、 y 和 y_grad 與計算圖中節點的對應關係,我們將這些變數節點輸出,可見:
x:<tf.Variable 'x:0' shape=() dtype=float32>y:Tensor("Square:0", shape=(), dtype=float32)y_grad:[<tf.Tensor 'gradients/Square_grad/Mul_1:0' shape=() dtype=float32>]
在 TensorBoard 中,我們也可以通過點擊節點獲得節點名稱。通過比較我們可以得知,變數 x 對應計算圖最下方的x,節點 y 對應計算圖「Square」塊的「 (Square) 」,節點 y_grad 對應計算圖上方「Square_grad」的 Mul_1 節點。同時我們還可以通過點擊節點發現,「Square_grad」塊里的const節點值為2,「gradients」塊里的 grad_ys_0 值為1, Shape 值為空,以及「x」塊的const節點值為3。
接下來,我們開始具體分析這個計算圖的結構。我們可以注意到,這個計算圖的結構是比較清晰的,「x」塊負責變數的讀取和初始化,「Square」塊負責求平方 y = x ^ 2 ,而「gradients」塊則負責對「Square」塊的操作求導,即計算 y_grad = 2 * x。由此我們可以看出, tf.gradients 是一個相對比較「龐大」的操作,並非如一般的操作一樣往計算圖中添加了一個或幾個節點,而是建立了一個龐大的子圖,以應用鏈式法則求計算圖中特定節點的導數。
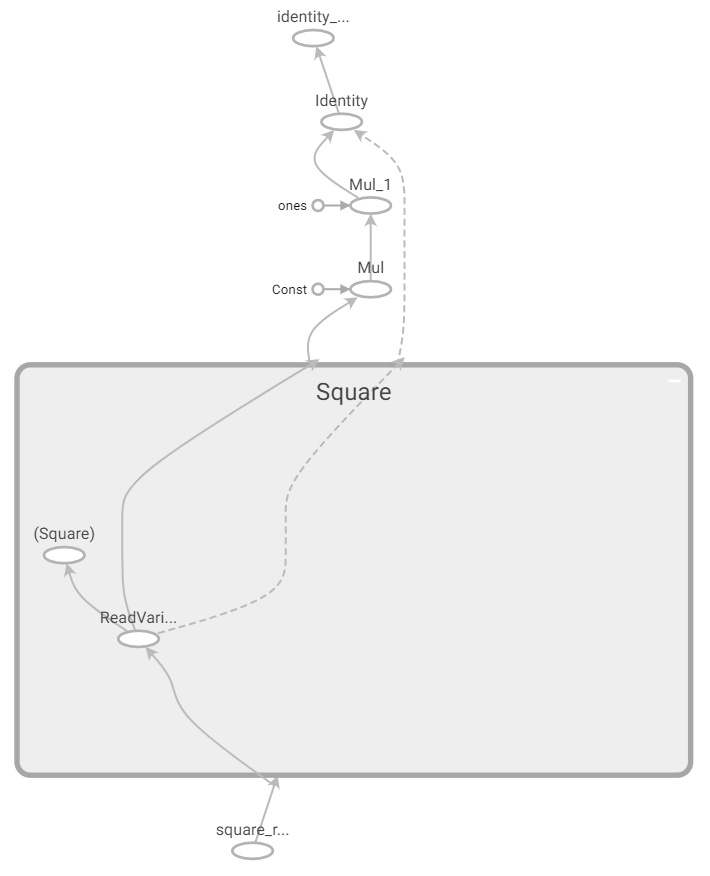
在 TensorFlow 2 的圖執行模式 API 中,將生成的計算圖使用 TensorBoard 進行展示:
我們可以注意到,除了求導過程沒有封裝在「gradients」塊內,以及變數的處理簡化以外,其他的區別並不大。由此,我們可以看出,在圖執行模式下, tf.GradientTape 這一上下文管理器的 gradient 方法和 TensorFlow 1.X 的 tf.gradients 是基本等價的。
小結
TensorFlow 1.X 中的 tf.gradients 和 TensorFlow 2 圖執行模式下的 tf.GradientTape 上下文管理器儘管在 API 層面的呼叫方法略有不同,但最終生成的計算圖是基本一致的。
基礎示例:線性回歸¶
在本節,我們為 第一章的線性回歸示例 提供一個基於 TensorFlow 1.X 的圖執行模式 API 的版本,供有需要的讀者對比參考。
與第一章的NumPy和即時執行模式不同,TensorFlow的圖執行模式使用 符號式編程 來進行數值運算。首先,我們需要將待計算的過程抽象為計算圖,將輸入、運算和輸出都用符號化的節點來表達。然後,我們將資料不斷地送入輸入節點,讓資料沿著計算圖進行計算和流動,最終到達我們需要的特定輸出節點。
以下程式碼展示了如何基於 TensorFlow 的符號編譯方法完成與前節相同的任務。其中, tf.placeholder() 即可以視為一種「符號化的輸入節點」,使用 tf.get_variable() 定義模型的參數(Variable類型的張量可以使用 tf.assign() 操作進行賦值),而 sess.run(output_node, feed_dict={input_node: data}) 可以視作將資料送入輸入節點,沿著計算圖計算併到達輸出節點並返回值的過程。
import tensorflow as tf
# 定義資料流圖
learning_rate_ = tf.placeholder(dtype=tf.float32)
X_ = tf.placeholder(dtype=tf.float32, shape=[5])
y_ = tf.placeholder(dtype=tf.float32, shape=[5])
a = tf.get_variable('a', dtype=tf.float32, shape=[], initializer=tf.zeros_initializer)
b = tf.get_variable('b', dtype=tf.float32, shape=[], initializer=tf.zeros_initializer)
y_pred = a * X_ + b
loss = tf.constant(0.5) * tf.reduce_sum(tf.square(y_pred - y_))
# 反向傳播,手動計算變數(模型參數)的梯度
grad_a = tf.reduce_sum((y_pred - y_) * X_)
grad_b = tf.reduce_sum(y_pred - y_)
# 梯度下降法,手動更新參數
new_a = a - learning_rate_ * grad_a
new_b = b - learning_rate_ * grad_b
update_a = tf.assign(a, new_a)
update_b = tf.assign(b, new_b)
train_op = [update_a, update_b]
# 資料流圖定義到此結束
# 注意,直到目前,我們都沒有進行任何實質的資料計算,僅僅是定義了一個資料流圖
num_epoch = 10000
learning_rate = 1e-3
with tf.Session() as sess:
# 初始化變數a和b
tf.global_variables_initializer().run()
# 迴圈將資料送入上面建立的資料流圖中進行計算和更新變數
for e in range(num_epoch):
sess.run(train_op, feed_dict={X_: X, y_: y, learning_rate_: learning_rate})
print(sess.run([a, b]))
自動求導機制¶
在上面的兩個示例中,我們都是人工計算獲得損失函數關於各參數的偏導數。但當模型和損失函數都變得十分複雜時(尤其是深度學習模型),這種人工求導的工作量就難以接受了。因此,在圖執行模式中,TensorFlow同樣提供了 自動求導機制 。類似於即時執行模式下的 tape.grad(ys, xs) ,可以利用TensorFlow的求導操作 tf.gradients(ys, xs) 求出損失函數 loss 關於 a , b 的偏導數。由此,我們可以將上節中的兩行手工計算導數的程式碼
# 反向傳播,手動計算變數(模型參數)的梯度
grad_a = tf.reduce_sum((y_pred - y_) * X_)
grad_b = tf.reduce_sum(y_pred - y_)
替換為
grad_a, grad_b = tf.gradients(loss, [a, b])
計算結果將不會改變。
優化器¶
TensorFlow在圖執行模式下也附帶有多種 優化器 (optimizer),可以將求導和梯度更新一併完成。我們可以將上節的程式碼
# 反向傳播,手動計算變數(模型參數)的梯度
grad_a = tf.reduce_sum((y_pred - y_) * X_)
grad_b = tf.reduce_sum(y_pred - y_)
# 梯度下降法,手動更新參數
new_a = a - learning_rate_ * grad_a
new_b = b - learning_rate_ * grad_b
update_a = tf.assign(a, new_a)
update_b = tf.assign(b, new_b)
train_op = [update_a, update_b]
整體替換為
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate_)
grad = optimizer.compute_gradients(loss)
train_op = optimizer.apply_gradients(grad)
這裡,我們先實例化了一個TensorFlow中的梯度下降優化器 tf.train.GradientDescentOptimizer() 並設置學習率。然後利用其 compute_gradients(loss) 方法求出 loss 對所有變數(參數)的梯度。最後通過 apply_gradients(grad) 方法,根據前面算出的梯度來梯度下降更新變數(參數)。
以上三行程式碼等價於下面一行程式碼:
train_op = tf.train.GradientDescentOptimizer(learning_rate=learning_rate_).minimize(loss)
使用自動求導機制和優化器簡化後的程式碼如下:
import tensorflow as tf
learning_rate_ = tf.placeholder(dtype=tf.float32)
X_ = tf.placeholder(dtype=tf.float32, shape=[5])
y_ = tf.placeholder(dtype=tf.float32, shape=[5])
a = tf.get_variable('a', dtype=tf.float32, shape=[], initializer=tf.zeros_initializer)
b = tf.get_variable('b', dtype=tf.float32, shape=[], initializer=tf.zeros_initializer)
y_pred = a * X_ + b
loss = tf.constant(0.5) * tf.reduce_sum(tf.square(y_pred - y_))
# 反向传播,利用TensorFlow的梯度下降优化器自动计算并更新变量(模型参数)的梯度
train_op = tf.train.GradientDescentOptimizer(learning_rate=learning_rate_).minimize(loss)
num_epoch = 10000
learning_rate = 1e-3
with tf.Session() as sess:
tf.global_variables_initializer().run()
for e in range(num_epoch):
sess.run(train_op, feed_dict={X_: X, y_: y, learning_rate_: learning_rate})
print(sess.run([a, b]))