TensorFlow Quantum: 混合量子-經典機器學習 *¶
我們身邊的經典電腦利用位元和邏輯閘進行二進制運算。在物理硬體上,這種運算主要是通過半導體的特殊導電性質來實現。經過幾十年的發展,我們已經可以在一片小小的半導體晶片上有上億個晶體管,從而實現高性能的經典計算。
而量子計算(Quantum Computing)利用具有量子特性(例如量子疊加態和量子糾纏)的 “量子位元” 和 “量子閘” 進行計算。這種新的計算模式可以在搜索和大數分解等重要領域達成指數級的加速,讓當前無法實現的一些超大規模運算成為可能,在未來深遠的改變世界。在物理硬體上,這類量子運算也可以通過一些具有量子特性的結構(例如超導約瑟夫森結)來實現。
不幸的是,盡管量子計算的理論已經有了比較深入的發展,但在硬體上,我們目前仍然造不出一台超越經典電腦的通用量子電腦 1 。IBM 和谷歌等業界巨頭在通用量子電腦的物理構建上已經有一些不錯的成果,但無論是量子位元的個數還是在量子去相干問題的解決上,都還遠無法達到實用的層級。
以上是量子計算的基本背景,接下來我們討論量子機器學習。量子機器學習的一種最直接的思路是使用量子計算加速傳統的機器學習任務,例如量子版本的 PCA、SVM 和 K-Means 算法,然而這些算法目前都尚未達到可實用的程度。我們在本章討論的量子機器學習則朝向另一個思考方向,即建構參數化的量子電路(Parameterized Quantum Circuits, PQCs)。PQC 可以使用在深度學習模型中的層,如果我們在普通深度學習模型的基礎上加入 PQC,即稱為混合量子 - 經典機器學習(Hybrid Quantum-Classical Machine Learning)。這種混合模型非常適合於量子資料集(Quantum Data)上的任務。而 TensorFlow Quantum 正是幫助我們構建這種混合量子 - 經典機器學習模型的利器。接下來,我們會對量子計算許多種的基本概念進行簡介,然後介紹使用 TensorFlow Quantum 和谷歌的量子計算函式庫 Cirq 構建 PQC、將 PQC 嵌入 Keras 模型、並在量子資料集上訓練混合模型的流程。
量子計算基本概念¶
本節將簡述量子計算的一些基本概念,包括量子位元、量子閘、量子電路等。
推薦閱讀
如果你希望更深入的了解量子力學以及量子計算的基本原理,建議可以從以下資源學習:
Griffiths, D., & Schroeter, D. (2018). Introduction to Quantum Mechanics . Cambridge: Cambridge University Press. doi:10.1017/9781316995433
Hidary, Jack D. Quantum Computing: An Applied Approach . Cham: Springer International Publishing, 2019. https://doi.org/10.1007/978-3-030-23922-0. (注重程式碼實操的量子計算教程,GitHub 上有配套源碼: https://github.com/JackHidary/quantumcomputingbook )
量子位元¶
在二進制的經典電腦中,我們用位元(Bit,也稱 “位元”)作為資料儲存的基本單位,一個位元只有 0 或 1 兩種狀態。而在量子電腦中,我們使用量子位元(Quantum Bit, Qubit,也稱 “量子位元”)進行資料的表示。量子位元也有兩種基本狀態 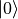 和
和 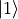 。不過量子位元除了可以處於這兩種基本狀態以外,還可以處於兩者之間的疊加態(Superposition State),即
。不過量子位元除了可以處於這兩種基本狀態以外,還可以處於兩者之間的疊加態(Superposition State),即 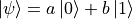 (其中a和b是複數,
(其中a和b是複數, 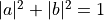 )。例如,
)。例如, 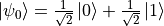 和
和 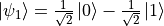 都是合法的量子狀態。我們也可以使用向量化的語言來表示量子位元的狀態。如果我們令
都是合法的量子狀態。我們也可以使用向量化的語言來表示量子位元的狀態。如果我們令 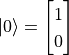 、
、 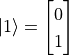 ,則
,則 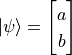 、
、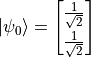 、
、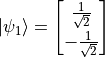 。
。
同時,我們可以用布洛赫球面(Bloch Sphere)來展示單個量子位元的狀態。球面的最頂端為 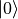 ,最底端為
,最底端為  ,而從原點到球面上任何一點的單位向量都可以是一個量子位元的狀態。
,而從原點到球面上任何一點的單位向量都可以是一個量子位元的狀態。
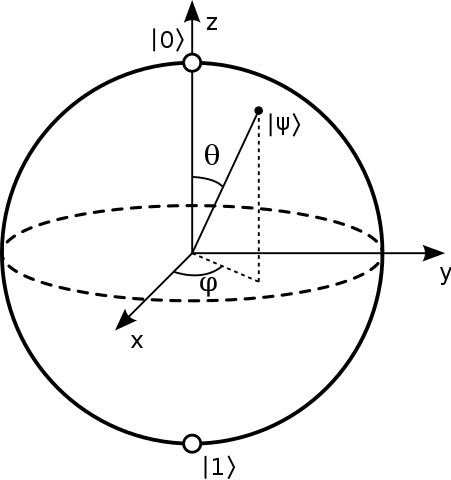
布洛赫球面( Bloch Sphere )。其中Z軸正負方向的量子態分別爲基本態 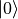 和
和 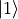 ,X軸正負方向的量子態分別爲
,X軸正負方向的量子態分別爲 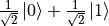 和
和 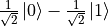 ,Y軸正負方向的量子態分別爲
,Y軸正負方向的量子態分別爲 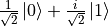 和
和 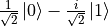 。圖示來源¶
。圖示來源¶
值得特別注意的是,儘管量子位元 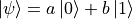 可能的狀態相當之多,但一旦我們對其進行觀測,則其狀態會立即坍縮 2 到
可能的狀態相當之多,但一旦我們對其進行觀測,則其狀態會立即坍縮 2 到 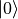 和
和 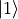 這兩個基本狀態中的一個,其概率分別爲
這兩個基本狀態中的一個,其概率分別爲 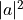 和
和 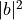 。
。
量子邏輯閘¶
在二進制的經典電腦中,我們有 AND、OR、NOT等邏輯閘,對輸入的位元狀態進行變換並輸出。在量子電腦中,我們同樣有量子邏輯閘(Quantum Logic Gate,或簡稱 “量子閘”),對量子狀態進行變換並輸出。如果我們使用向量化的語言來表述量子狀態,則量子邏輯閘可以看作是一個對狀態向量進行變換的矩陣。
例如,量子NOT閘可以表達成 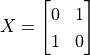 ,於是當我們將量子NOT閘作用於基本態
,於是當我們將量子NOT閘作用於基本態 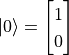 時,我們得到
時,我們得到 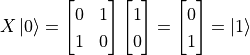 。量子閘也可以作用在疊加態,例如
。量子閘也可以作用在疊加態,例如 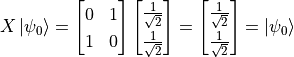 (這說明量子NOT閘沒能改變量子態
(這說明量子NOT閘沒能改變量子態 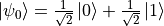 的狀態。事實上,量子NOT閘
的狀態。事實上,量子NOT閘 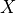 相當於在布洛赫球面上將量子態繞X軸旋轉180度。而
相當於在布洛赫球面上將量子態繞X軸旋轉180度。而 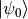 就在X軸上,所以沒有變化)。量子AND閘和OR閘 3 由於涉及到多個量子位元而稍顯複雜,但同樣可以通過尺寸更大的矩陣實現。
就在X軸上,所以沒有變化)。量子AND閘和OR閘 3 由於涉及到多個量子位元而稍顯複雜,但同樣可以通過尺寸更大的矩陣實現。
可能有些讀者已經想到了,既然單個量子位元的狀態不止 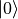 和
和 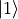 兩種,那麼量子邏輯閘作為作為對量子位元的變換,其實也完全可以不局限於AND或NOT。事實上,只要滿足一定條件的矩陣 4 都可以作為量子邏輯閘。例如,將量子態在布洛赫球面上繞 X、Y、Z 軸旋轉的變換:math:Rx(theta) 、
兩種,那麼量子邏輯閘作為作為對量子位元的變換,其實也完全可以不局限於AND或NOT。事實上,只要滿足一定條件的矩陣 4 都可以作為量子邏輯閘。例如,將量子態在布洛赫球面上繞 X、Y、Z 軸旋轉的變換:math:Rx(theta) 、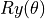 、
、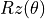 (其中
(其中 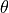 是旋轉角度,當
是旋轉角度,當 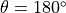 時記爲
時記爲 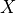 、
、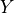 、
、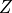 )都是量子邏輯閘。另外,有一個量子邏輯閘「阿達馬閘」(Hadamard Gate)
)都是量子邏輯閘。另外,有一個量子邏輯閘「阿達馬閘」(Hadamard Gate) 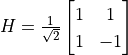 可以將量子狀態從基本態轉換爲疊加態,在很多量子計算的場景中占據了重要地位。
可以將量子狀態從基本態轉換爲疊加態,在很多量子計算的場景中占據了重要地位。
量子電路¶
當我們將量子位元以及量子邏輯閘按順序標記在一條或多條平行的線條上時,就構成了量子電路(Quantum Circuit,或稱量子電路)。例如,對於我們在上一節討論的,使用量子NOT閘 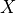 對基本態
對基本態 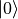 進行變換的過程,我們可以寫出量子電路如下:
進行變換的過程,我們可以寫出量子電路如下:
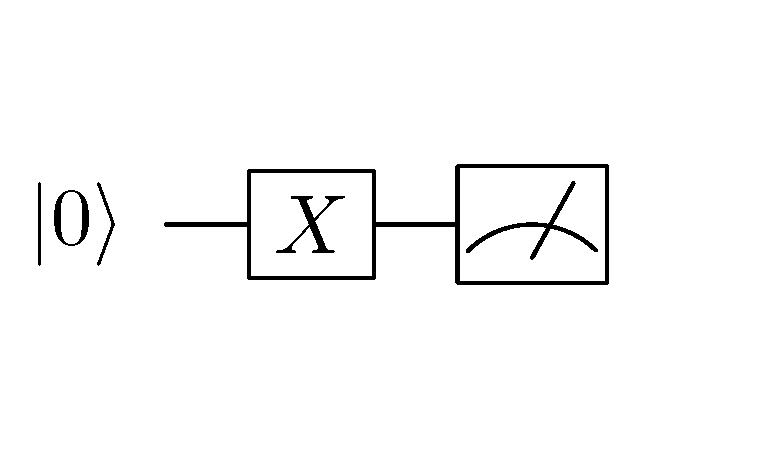
一個簡單的量子電路¶
在量子電路中,每條橫線代表一個量子位元。上圖中最左邊的 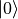 代表量子位元的初始態。中間的X方塊代表量子NOT閘
代表量子位元的初始態。中間的X方塊代表量子NOT閘 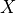 ,最右邊的錶盤符號代表測量操作。這個電路的意義是「對初始狀態爲
,最右邊的錶盤符號代表測量操作。這個電路的意義是「對初始狀態爲 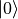 的量子位元執行量子NOT閘
的量子位元執行量子NOT閘 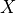 操作,並測量變換後的量子位元狀態」。根據我們在前面章節的討論,變換後的量子位元狀態為基本態
操作,並測量變換後的量子位元狀態」。根據我們在前面章節的討論,變換後的量子位元狀態為基本態 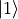 ,因此我們可以期待該量子電路最後的測量結果始終為 1。
,因此我們可以期待該量子電路最後的測量結果始終為 1。
接下來,我們考慮將上圖中量子電路的量子NOT閘 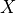 換爲阿達馬閘
換爲阿達馬閘 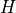 :
:
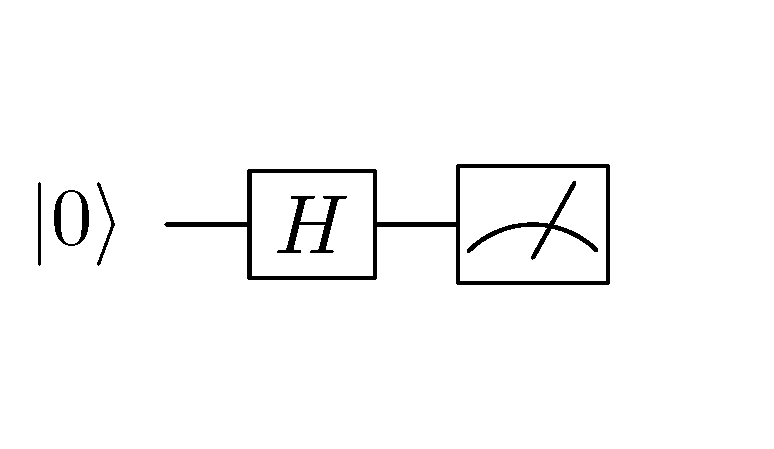
將量子NOT閘 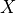 換爲阿達馬閘
換爲阿達馬閘 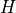 後的量子電路¶
後的量子電路¶
阿達馬閘(Hadamard gate)對應的矩陣表示為 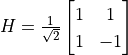 ,於是我們可以計算出變換後的量子態為
,於是我們可以計算出變換後的量子態為 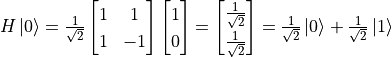 。這是一個
。這是一個 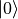 和
和 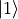 的疊加態,在觀測後會坍縮(Collapse)到基本態,其機率分別為
的疊加態,在觀測後會坍縮(Collapse)到基本態,其機率分別為 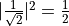 。也就是說,這個量子電路的觀測結果類似於扔硬幣。假若觀測 20 次,則大約 10 次的結果是
。也就是說,這個量子電路的觀測結果類似於扔硬幣。假若觀測 20 次,則大約 10 次的結果是 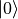 ,10次的結果是
,10次的結果是 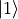 。
。
實例:使用Cirq建立簡單的量子電路¶
Cirq 是谷歌主導的開源量子計算函式庫,可以幫助我們方便的建立量子電路並模擬測量結果(我們在下一節介紹 TensorFlow Quantum 的時候還會用到它)。Cirq 是一個 Python 函式庫,可以使用 pip install cirq 進行安裝。以下程式碼實現了上一個章節所建立的兩個簡單的量子電路,並分別進行了 20 次的模擬測量。
import cirq
q = cirq.LineQubit(0) # 實例化一個量子位元
simulator = cirq.Simulator() # 實例化一個模擬器
X_circuit = cirq.Circuit( # 建立一個包含量子NOT閘和測量的量子電路
cirq.X(q),
cirq.measure(q)
)
print(X_circuit) # 在終端可視化輸出量子電路
# 使用模擬器對該量子電路進行20次的模擬測量
result = simulator.run(X_circuit, repetitions=20)
print(result) # 輸出模擬測量結果
H_circuit = cirq.Circuit( # 建立一個包含阿達馬閘和測量的量子電路
cirq.H(q),
cirq.measure(q)
)
print(H_circuit)
result = simulator.run(H_circuit, repetitions=20)
print(result)
結果如下:
0: ───X───M───
0=11111111111111111111
0: ───H───M───
0=00100111001111101100
可見第一個量子電路的測量結果始終為 1,第二個量子態的 20 次測量結果中有 9 次是 0,11 次是 1(如果你多運行幾次,會發現 0 和 1 出現的機率趨近於  )。可見結果符合我們在上節中的分析。
)。可見結果符合我們在上節中的分析。
混合量子-經典機器學習¶
本節介紹混合量子 - 經典機器學習的基本概念,以及使用 TensorFlow Quantum 建立此類模型的方法。
在混合量子 - 經典機器學習過程中,我們使用量子資料集訓練混合量子 - 經典模型。混合量子 - 經典模型的前半部分是量子模型(即參數化的量子電路)。量子模型接受量子資料集作為輸入,對輸入使用量子閘進行變換,然後通過測量轉換為經典資料。測量後的經典資料輸入經典模型,並使用常規的損失函數計算模型的損失值。最後,基於損失函數的值計算模型參數的梯度並更新模型參數。整個過程不僅包括經典模型的參數,也包括量子模型的參數。具體流程如下圖所示。
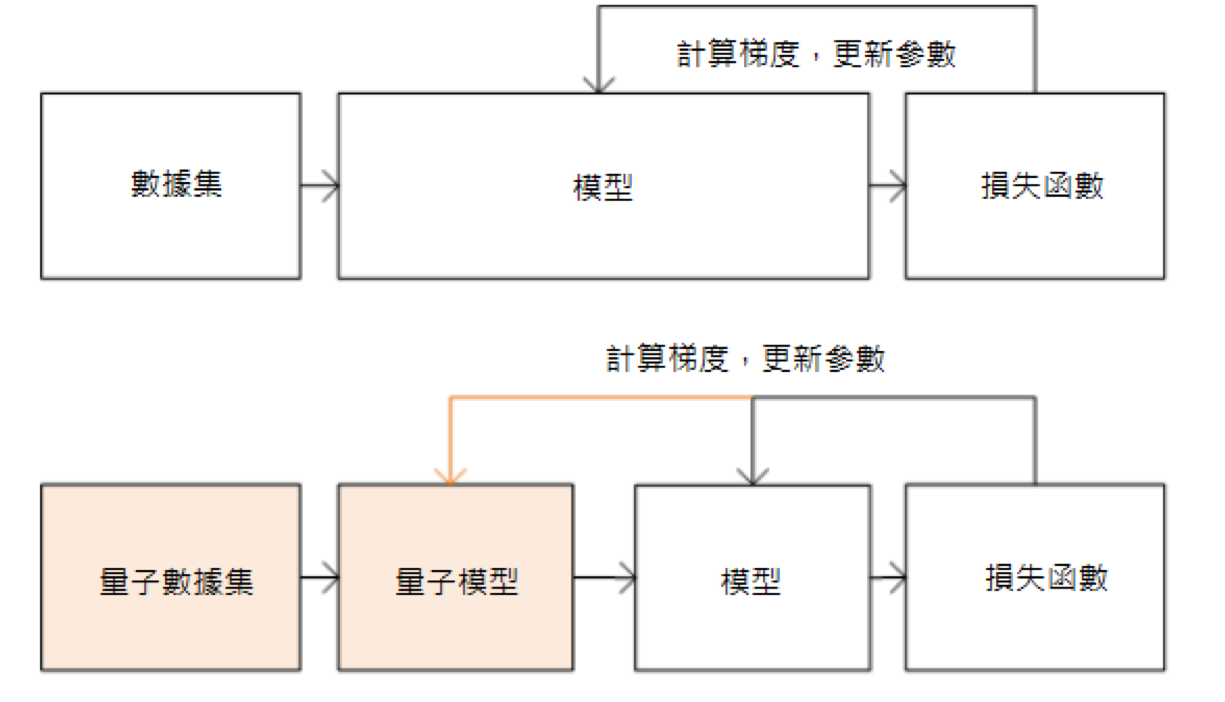
經典機器學習(上圖)與混合量子-經典機器學習(下圖)的流程對比¶
TensorFlow Quantum 即是一個與 TensorFlow Keras 結合緊密的,可快速建立混合量子 - 經典機器學習模型的開源函式庫,可以使用 pip install tensorflow-quantum 進行安裝。
後文範例默認使用以下程式碼導入 TensorFlow、TensorFlow Quantum 和 Cirq:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
推薦閱讀
Broughton, Michael, Guillaume Verdon, Trevor McCourt, Antonio J. Martinez, Jae Hyeon Yoo, Sergei V. Isakov, Philip Massey, et al. 「 TensorFlow Quantum: A Software Framework for Quantum Machine Learning. 」 ArXiv:2003.02989 [Cond-Mat, Physics:Quant-Ph], March 5, 2020. (TensorFlow Quantum 白皮書)
量子資料集與包含參數的量子閘¶
監督式學習為例,資料集由資料和標籤組成。資料中的每一項是一個由不同特徵組成的向量。我們可以將資料集寫作 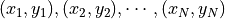 ,其中
,其中 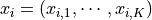 。量子資料集同樣由資料和標籤組成,而資料中的每一項是一個量子態。以前面章節單量子位元的量子態為例,我們可以將每一項資料寫作
。量子資料集同樣由資料和標籤組成,而資料中的每一項是一個量子態。以前面章節單量子位元的量子態為例,我們可以將每一項資料寫作 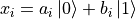 。在具體實現上,我們可以通過量子電路來生成量子資料。也就是說,每一項資料
。在具體實現上,我們可以通過量子電路來生成量子資料。也就是說,每一項資料 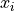 都對應著一個量子電路。例如,我們可以通過以下程式碼,使用 Cirq 生成一組量子資料:
都對應著一個量子電路。例如,我們可以通過以下程式碼,使用 Cirq 生成一組量子資料:
q = cirq.GridQubit(0, 0)
q_data = []
for i in range(100):
x_i = cirq.Circuit(
cirq.rx(np.random.rand() * np.pi)(q)
)
q_data.append(x_i)
在這個過程中,我們使用了一個帶參數的量子閘 cirq.rx(angle)(q) 。和之前我們使用的量子閘 cirq.X(q) , cirq.H(q) 不同的是,這個量子閘多了一個參數 angle ,表示將量子位元 q 繞布洛赫球面的 x 軸旋轉 angle 角度。以上程式碼生成了 100 項量子資料,每項資料是從基本態 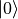 開始繞布洛赫球面的x軸隨機旋轉
開始繞布洛赫球面的x軸隨機旋轉 ![[0, \pi]](../../_images/math/b61438f8e15d426e93bf63b6c39c296435cdacaf.png) 角度所變換而來的量子態。量子資料集在不少量子相關的領域(如化學、材料科學、生物學和藥物發現等)都有應用。
角度所變換而來的量子態。量子資料集在不少量子相關的領域(如化學、材料科學、生物學和藥物發現等)都有應用。
當我們要將量子資料集作為 Keras 的輸入時,可以使用 TensorFlow Quantum 的 convert_to_tensor 方法,將量子資料集轉換為張量:
q_data = tfq.convert_to_tensor(q_data)
值得注意的是,當使用量子資料集作為 Keras 模型的訓練資料時,Keras 模型的輸入類型( dtype )需要為 tf.dtypes.string 。
參數化的量子電路(PQC)¶
當我們在建立量子電路時使用了帶參數的量子閘,該參數可以自由調整,我們稱這樣的量子電路為參數化的量子電路。Cirq 支持結合 SymPy 這一 Python 下的符號運算函式庫實現參數化的量子電路,範例如下
import sympy
theta = sympy.Symbol('theta')
q_model = cirq.Circuit(cirq.rx(theta)(q))
在上面的程式碼中,我們建立了如下圖所示的量子電路。該量子電路可以將任意輸入量子態 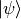 繞布洛赫球面的x軸逆時針旋轉
繞布洛赫球面的x軸逆時針旋轉 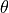 度,其中
度,其中 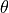 是使用
是使用 sympy.Symbol 宣告的符號變數(即參數)。
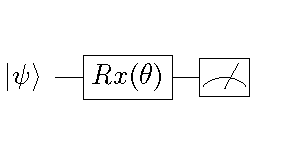
參數化的量子電路範例¶
將參數化的量子電路嵌入機器學習模型¶
通過 TensorFlow Quantum,我們可以輕鬆的將參數化的量子電路以 Keras 層的方式嵌入 Keras 模型。例如前面章節建立的參數化的量子電路 q_model ,我們可以使用 tfq.layers.PQC 將其直接作為一個 Keras 層使用
q_layer = tfq.layers.PQC(q_model, cirq.Z(q))
expectation_output = q_layer(q_data_input)
tfq.layers.PQC 的第一個參數為使用 Cirq 建立的參數化的量子電路,第二個參數為測量方式,此處使用 cirq.Z(q) 在布洛赫球面的 Z 軸進行測量。
以上程式碼也可直接寫作:
expectation_output = tfq.layers.PQC(q_model, cirq.Z(q))(q_data_input)
範例:對量子資料集進行二分類¶
在以下程式碼中,我們首先建立了一個量子資料集,其中一半的資料為基本態 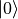 繞布洛赫球面的x軸逆時針旋轉
繞布洛赫球面的x軸逆時針旋轉 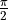 弧度(即
弧度(即 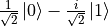 ),另一半則為
),另一半則為 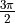 弧度(即
弧度(即 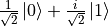 )。所有的資料均加入了繞 x,y 軸方向旋轉的,標準差為
)。所有的資料均加入了繞 x,y 軸方向旋轉的,標準差為 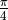 的高斯噪聲。對於這個量子資料集,如果不加變換而直接測量,則所有資料都會和拋硬幣一樣等機率隨機坍縮到基本態
的高斯噪聲。對於這個量子資料集,如果不加變換而直接測量,則所有資料都會和拋硬幣一樣等機率隨機坍縮到基本態 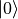 和
和 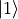 ,從而無法區分。
,從而無法區分。
為了區分這兩類資料,我們接下來建立了一個量子模型,這個模型將單位元量子態繞布洛赫球面的 x 軸逆時針旋轉 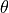 角度。變換過後量子態資料的測量值送入 “全連接層 + softmax” 的經典機器學習模型,並使用交叉熵作為損失函數。模型訓練過程會自動同時調整量子模型中
角度。變換過後量子態資料的測量值送入 “全連接層 + softmax” 的經典機器學習模型,並使用交叉熵作為損失函數。模型訓練過程會自動同時調整量子模型中 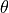 的值和全連接層的權重值,使得整個混合量子 - 經典機器學習模型的準確度較高。
的值和全連接層的權重值,使得整個混合量子 - 經典機器學習模型的準確度較高。
import cirq
import sympy
import numpy as np
import tensorflow as tf
import tensorflow_quantum as tfq
q = cirq.GridQubit(0, 0)
# 準備量子資料集(q_data, label)
add_noise = lambda x: x + np.random.normal(0, 0.25 * np.pi)
q_data = tfq.convert_to_tensor(
[cirq.Circuit(
cirq.rx(add_noise(0.5 * np.pi))(q),
cirq.ry(add_noise(0))(q)
) for _ in range(100)] +
[cirq.Circuit(
cirq.rx(add_noise(1.5 * np.pi))(q),
cirq.ry(add_noise(0))(q)
) for _ in range(100)]
)
label = np.array([0] * 100 + [1] * 100)
# 建立參數化的量子電路(PQC)
theta = sympy.Symbol('theta')
q_model = cirq.Circuit(cirq.rx(theta)(q))
# 建立量子層和經典全連接層
q_layer = tfq.layers.PQC(q_model, cirq.Z(q))
dense_layer = tf.keras.layers.Dense(2, activation=tf.keras.activations.softmax)
# 使用Keras建立訓練流程。量子資料首先通過PQC,然後通過經典的全連接模型
q_data_input = tf.keras.Input(shape=() ,dtype=tf.dtypes.string)
expectation_output = q_layer(q_data_input)
classifier_output = dense_layer(expectation_output)
model = tf.keras.Model(inputs=q_data_input, outputs=classifier_output)
# 編譯模型,指定優化器、損失函數和評估指標,並進行訓練
model.compile(
optimizer=tf.keras.optimizers.SGD(learning_rate=0.01),
loss=tf.keras.losses.sparse_categorical_crossentropy,
metrics=[tf.keras.metrics.sparse_categorical_accuracy]
)
model.fit(x=q_data, y=label, epochs=200)
# 輸出量子層參數(即theta)的訓練結果
print(q_layer.get_weights())
輸出:
...
200/200 [==============================] - 0s 165us/sample - loss: 0.1586 - sparse_categorical_accuracy: 0.9500
[array([-1.5279944], dtype=float32)]
可以發現,通過訓練,模型在訓練集上可以達到 95% 的準確率, 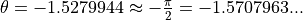 。而當
。而當 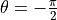 時,恰好可以使得兩種類型的資料分別接近基本態
時,恰好可以使得兩種類型的資料分別接近基本態 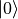 和
和 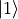 ,從而達到最易區分的狀態。
,從而達到最易區分的狀態。