TensorFlow 基礎¶
本章介紹 TensorFlow 的基本操作。
前置知識
Python 基本操作 (賦值、程式分支及控制流程、使用 import 導入套件);
NumPy ,Python 下常用的科學計算套件。TensorFlow 與之結合緊密;
線性迴歸 ;
梯度下降方法 求函數的局部最小值。
TensorFlow 1+1¶
我們可以先簡單地將 TensorFlow 視為一個科學計算套件(類似於 Python 下的 NumPy)。
首先,我們導入 TensorFlow:
import tensorflow as tf
警告
本手冊基於 TensorFlow 的即時執行模式(Eager Execution)。在 TensorFlow 1.X 版本中, 必須 在導入 TensorFlow 套件後呼叫 tf.enable_eager_execution() 函數以啟用即時執行模式。在 TensorFlow 2 中,即時執行模式將成為預設模式,無需額外呼叫 tf.enable_eager_execution() 函數(不過若要關閉即時執行模式,則需呼叫 tf.compat.v1.disable_eager_execution() 函数)。
TensorFlow 使用 **張量**(Tensor)作為資料的基本單位。TensorFlow 的張量在概念上等同於多維陣列,我們可以使用它來描述數學中的純量(0 維陣列)、向量(1 維陣列)、矩陣(2 維陣列)等各種量,範例如下:
# 定義一個隨機數(純量)
random_float = tf.random.uniform(shape=())
# 定義一個有2個元素的零向量
zero_vector = tf.zeros(shape=(2))
# 定義兩個2×2的常量矩陣
A = tf.constant([[1., 2.], [3., 4.]])
B = tf.constant([[5., 6.], [7., 8.]])
張量的重要屬性是其形狀、類型和值。可以通過張量的 shape 、 dtype 屬性和 numpy() 方法獲得。例如:
# 查看矩陣A的形狀、類型和值
print(A.shape) # 輸出(2, 2),即矩陣的長和寬均為2
print(A.dtype) # 輸出<dtype: 'float32'>
print(A.numpy()) # 輸出[[1. 2.]
# [3. 4.]]
小技巧
TensorFlow 的大多數 API 函數會根據輸入的值自動推斷張量中元素的類型(一般預設為 tf.float32 )。不過你也可以通過加入 dtype 參數來自行指定類型,例如 zero_vector = tf.zeros(shape=(2), dtype=tf.int32) 將使得張量中的元素類型均為整數。張量的 numpy() 方法是將張量的值轉換為一個 NumPy 陣列。
TensorFlow 裡有大量的運算函數(Operation),使得我們可以將已有的張量進行運算後得到新的張量。範例如下:
C = tf.add(A, B) # 計算矩陣A和B的和
D = tf.matmul(A, B) # 計算矩陣A和B的乘積
操作完成後, C 和 D 的值分別為:
tf.Tensor(
[[ 6. 8.]
[10. 12.]], shape=(2, 2), dtype=float32)
tf.Tensor(
[[19. 22.]
[43. 50.]], shape=(2, 2), dtype=float32)
可見,我們成功使用 tf.add() 操作計算出 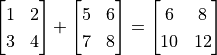 ,使用
,使用 tf.matmul() 操作計算出 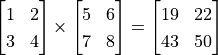 。
。
自動推導機制¶
在機器學習中,我們經常需要計算函數的導數。TensorFlow 提供了強大的 自動推導機制 来计算导数。來計算導數。在即時執行模式下,TensorFlow 引入了 tf.GradientTape() 這個“推導記錄器”來實現自動微分。以下程式碼展示了如何使用 tf.GradientTape() 計算函數 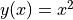 在
在 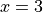 時的導數:
時的導數:
import tensorflow as tf
x = tf.Variable(initial_value=3.)
with tf.GradientTape() as tape: # 在 tf.GradientTape() 的上下文內,所有計算步驟都會被記錄以用於推導
y = tf.square(x)
y_grad = tape.gradient(y, x) # 計算y關於x的導數
print(y, y_grad)
輸出:
tf.Tensor(9.0, shape=(), dtype=float32)
tf.Tensor(6.0, shape=(), dtype=float32)
這裡 x 是一個初始化為 3 的 變數 (Variable),使用 tf.Variable() 宣告。與普通張量一樣,變數同樣具有形狀、類型和值三種屬性。使用變數需要有一個初始化過程,可以通過在 tf.Variable() 中指定 initial_value 參數來指定初始值。這裡將變數 x 初始化為 3. 1。變數與普通張量的一個重要區別是其預設能夠被 TensorFlow 的自動推導機制所求,因此往往被用於定義機器學習模型的參數。
tf.GradientTape() 是一個自動推導的記錄器。只要進入了 with tf.GradientTape() as tape 的上下文環境,則在該環境中計算步驟都會被自動記錄。比如在上面的範例中,計算步驟 y = tf.square(x) 即被自動記錄。離開上下文環境後,記錄將停止,但記錄器 tape 依然可用,因此可以通過 y_grad = tape.gradient(y, x) 求張量 y 對變數 x 的導數。
在機器學習中,更加常見的是對多元函數求偏導數,以及對向量或矩陣的推導。這些對於 TensorFlow 也不在話下。以下程式碼展示了如何使用 tf.GradientTape() 計算函數 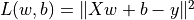 在
在 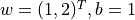 時分別對
時分別對 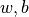 的偏導數。其中
的偏導數。其中 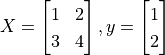 。
。
X = tf.constant([[1., 2.], [3., 4.]])
y = tf.constant([[1.], [2.]])
w = tf.Variable(initial_value=[[1.], [2.]])
b = tf.Variable(initial_value=1.)
with tf.GradientTape() as tape:
L = tf.reduce_sum(tf.square(tf.matmul(X, w) + b - y))
w_grad, b_grad = tape.gradient(L, [w, b]) # 計算L(w, b)關於w, b的偏導數
print(L, w_grad, b_grad)
輸出:
tf.Tensor(125.0, shape=(), dtype=float32)
tf.Tensor(
[[ 70.]
[100.]], shape=(2, 1), dtype=float32)
tf.Tensor(30.0, shape=(), dtype=float32)
這裡, tf.square() 操作代表對輸入張量的每一個元素求平方,不改變張量形狀。 tf.reduce_sum() 操作代表對輸入張量的所有元素求和,輸出一個形狀為空的純量張量(可以通過 axis 參數來指定求和的維度,不指定則預設對所有元素求和)。TensorFlow 中有大量的張量操作 API,包括數學運算、張量形狀操作(如 tf.reshape())、切片和連接(如 tf.concat())等多種類型,可以通過查閱 TensorFlow 的官方 API 文件 2 來進一步了解。
從輸出可見,TensorFlow 幫助我們計算出了
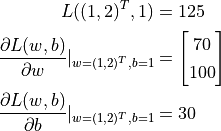
基礎範例:線性回歸¶
基礎知識和原理
UFLDL 教程 Linear Regression 一節。
考慮一個實際問題,某城市在 2013 年 - 2017 年的房價如下表所示:
年份 |
2013 |
2014 |
2015 |
2016 |
2017 |
房價 |
12000 |
14000 |
15000 |
16500 |
17500 |
現在,我們希望通過對該資料進行線性回歸,即使用線性模型 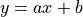 來擬合上述資料,此處
來擬合上述資料,此處 a 和 b 是待求的參數。
首先,我們定義資料,進行基本的正規化操作。
import numpy as np
X_raw = np.array([2013, 2014, 2015, 2016, 2017], dtype=np.float32)
y_raw = np.array([12000, 14000, 15000, 16500, 17500], dtype=np.float32)
X = (X_raw - X_raw.min()) / (X_raw.max() - X_raw.min())
y = (y_raw - y_raw.min()) / (y_raw.max() - y_raw.min())
接下來,我們使用梯度下降方法來求線性模型中兩個參數 a 和 b 的值 3。
回顧機器學習的基礎知識,對於多元函數 求局部極小值,梯度下降 的過程如下:
初始化自變數為
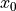 ,
, 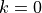
疊代進行下列步驟直到滿足收斂條件:
求函数
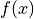 關於自變數的梯度
關於自變數的梯度 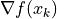
更新自變數:
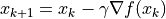 。這裡
。這裡 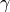 是學習率(也就是梯度下降一次邁出的“步長”大小)
是學習率(也就是梯度下降一次邁出的“步長”大小)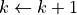
接下來,我們考慮如何使用程式來實現梯度下降方法,求得線性回歸的解 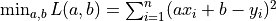 。
。
NumPy 下的線性回歸¶
機器學習模型的實現並不是 TensorFlow 的專利。事實上,對於簡單的模型,即使使用常規的科學計算套件或者工具也可以求解。在這裡,我們使用 NumPy 這一通用的科學計算套件來實現梯度下降方法。NumPy 提供了多維陣列支援,可以表示向量、矩陣以及更高維的張量。同時,也提供了大量支援在多維陣列上進行操作的函數(比如下面的 np.dot() 是求內積, np.sum() 是求和)。在這方面,NumPy 和 MATLAB 比較類似。在以下程式碼中,我們推導求損失函數關於參數 a 和 b 的偏導數 4,並使用梯度下降法反複疊代,最終獲得 a 和 b 的值。
a, b = 0, 0
num_epoch = 10000
learning_rate = 5e-4
for e in range(num_epoch):
# 手動計算損失函數關於自變數(模型參數)的梯度
y_pred = a * X + b
grad_a, grad_b = 2 * (y_pred - y).dot(X), 2 * (y_pred - y).sum()
# 更新參數
a, b = a - learning_rate * grad_a, b - learning_rate * grad_b
print(a, b)
然而,你或許已經可以注意到,使用常規的科學計算套件實現機器學習模型有兩個痛點:
經常需要人工推導求函數關於參數的偏導數。如果是簡單的函數或許還好,但一旦函數的形式變得複雜(尤其是深度學習模型),人工推導的過程將變得非常痛苦,甚至不可行。
經常需要人工根據推導的結果更新參數。這裡使用了最基礎的梯度下降方法,因此參數的更新還較為容易。但如果使用更加複雜的參數更新方法(例如 Adam 或者 Adagrad),這個更新過程的編寫同樣會非常繁雜。
而 TensorFlow 等深度學習框架的出現很大程度上解決了這些痛點,為機器學習模型的實現帶來了很大的便利。
TensorFlow下的線性回歸¶
TensorFlow的 即時執行模式 5 與上述 NumPy 的運行方式十分類似,然而提供了更快速的運算(GPU 支援)、自動推導、優化器等一系列對深度學習非常重要的功能。以下展示了如何使用 TensorFlow 計算線性回歸。可以注意到,程式的結構和前述 NumPy 的實現非常類似。這裡,TensorFlow 幫助我們做了兩件重要的工作:
使用
tape.gradient(ys, xs)自動計算梯度;使用
optimizer.apply_gradients(grads_and_vars)自動更新模型參數。
X = tf.constant(X)
y = tf.constant(y)
a = tf.Variable(initial_value=0.)
b = tf.Variable(initial_value=0.)
variables = [a, b]
num_epoch = 10000
optimizer = tf.keras.optimizers.SGD(learning_rate=5e-4)
for e in range(num_epoch):
# 使用tf.GradientTape()記錄損失函數的梯度資訊
with tf.GradientTape() as tape:
y_pred = a * X + b
loss = tf.reduce_sum(tf.square(y_pred - y))
# TensorFlow自動計算損失函數關於自變數(模型參數)的梯度
grads = tape.gradient(loss, variables)
# TensorFlow自動根據梯度更新參數
optimizer.apply_gradients(grads_and_vars=zip(grads, variables))
print(a, b)
在這裡,我們使用了前文的方式計算了損失函數關於參數的偏導數。同時,使用 tf.keras.optimizers.SGD(learning_rate=5e-4) 宣告了一個梯度下降 優化器 (Optimizer),其學習率為 5e-4。優化器可以幫助我們根據計算出的推導結果更新模型參數,從而最小化某個特定的損失函數,具體使用方式是呼叫其 apply_gradients() 方法。
注意到這裡,更新模型參數的方法 optimizer.apply_gradients() 需要提供参数 grads_and_vars,即待更新的變數(如上述程式碼中的 variables )及損失函數關於這些變數的偏導數(如上述程式碼中的 grads )。具體而言,這裡需要傳入一個 Python 列表(List),列表中的每個元素是一個 (變數的偏導數,變數) 對。比如上例中需要傳入的參數是 [(grad_a, a), (grad_b, b)] 。我們通過 grads = tape.gradient(loss, variables) 求出 tape 中記錄的 loss 關於 variables = [a, b] 中每個變數的偏導數,也就是 grads = [grad_a, grad_b],再使用Python的 zip() 函數將 grads = [grad_a, grad_b] 和 variables = [a, b] 結合在一起,就可以組合出所需的參數了。
Python的 zip() 函數
zip() 函數是 Python 的內建函數。用自然語言描述這個函數的功能很繞口,但如果舉個例子就很容易理解了:如果 a = [1, 3, 5], b = [2, 4, 6],那麼 zip(a, b) = [(1, 2), (3, 4), ..., (5, 6)] 。即 “將可疊代的對象作為參數,將對象中對應的元素打包成一個個元組,然組合後返回由這些組合組成的列表”,和我們日常生活中拉上拉鏈(zip)的操作有異曲同工之妙。在 Python 3 中, zip() 函數返回的是一個 zip 對象,本質上是一個生成器(Generator),需要呼叫 list() 來將生成器轉換成列表。
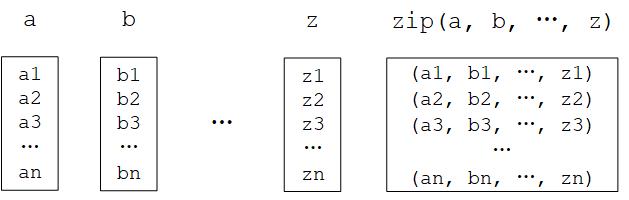
Python的 zip() 函數圖示¶
在實際應用中,我們編寫的模型往往比這裡一行就能寫完的線性模型 y_pred = a * X + b (模型參數為 variables = [a, b] )要複雜得多。所以,我們往往會編寫並實例化一個模型類 model = Model() ,然後使用 y_pred = model(X) 呼叫模型,使用 model.variables 獲取模型參數。關於模型類的編寫方式可見 “TensorFlow模型”一章。
- 1
Python 中可以使用整數後加小數點表示將該整數定義為浮點數類型。例如
3.代表浮點數3.0。- 2
主要可以參考 Tensor Transformations 頁面。可以注意到,TensorFlow 的張量操作 API 在形式上和 Python 下流行的科學計算套件 NumPy 非常類似,如果對後者有所了解的話可以快速上手。
- 3
其實線性回歸是有詳細解的。這裡使用梯度下降方法只是為了展示 TensorFlow 的運作方式。
- 4
此處的損失函數為均方誤差
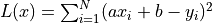 。其關於參數
。其關於參數 a和b的偏導數為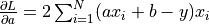 ,
,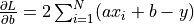 。本例中
。本例中 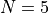 。由於均方誤差取均值的係數
。由於均方誤差取均值的係數 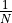 在訓練過程中一般為常數(
在訓練過程中一般為常數( 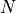 一般為批次大小),對損失函數乘以常數等價於調整學習率,因此在具體實現時通常不寫在損失函數中。
一般為批次大小),對損失函數乘以常數等價於調整學習率,因此在具體實現時通常不寫在損失函數中。- 5
與即時執行模式相對的是圖執行模式(Graph Execution),即 TensorFlow 2 之前所主要使用的執行模式。本手冊以面向快速疊代開發的即時執行模式為主,但會在 附錄中介紹圖執行模式的基本使用,供需要的讀者查閱。
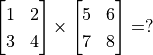 );
);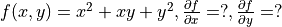 );
);